Bouclez vos ceintures je vous prie car nous sommes sur le point de subir une brutale ascension.
Nombreux sont ceux qui, au lieu de s’ancrer dans la richesse des abstractions d’un Cantor, d’un Dedekind, ou d’un Weierstrass, se perdent dans des considérations « très pop » sur les auteurs de celles-ci. S’attachant au « sexy » du contexte (la « folie » de Cantor, la bizarre normalité de Weierstrass), ils en oublient que la beauté de leurs abstractions se suffit à elle-même. Le mérite de D.F.Wallace est d’abord là. Il recentre sur l’essentiel, la chose mathématique, et nous rend accessible ce plaisir du vertige. Plaisir par lequel se vit et se comprend vraiment cette relation, intime depuis toujours, entre mathématique et philosophie.
Il me semble d’autant plus beau que sans aucune notion de quantités mesurables et simplement par un système fini de simples étapes de pensées, l’homme peut avancer vers la création du pur et continu domaine des nombres.
Le défi, dire les maths dans ce qu’elles proposent de plus abstrait à un public non expert , exprimer par elles-mêmes une réponse à la question : De quelle façon les abstractions existent-elles?, ce défi suppose, au-delà des connaissances évidentes en mathématiques, des qualités de poète. Car qui mieux que celui-ci peut comprendre l’enjeu qu’est faire vivre l’abstraction des mathématiques par celle du langage.
Tout ceci étant d’une bizarrerie absolument retentissante.
« Une histoire compacte de l’infini », comme il fait œuvre de science et de pédagogie, fait alors aussi œuvre littéraire. Car ce sont par ses procédés formels mêmes (redondances, interpellations humoristiques, mise en abyme des procédés rhétoriques) qu’il remplit parfaitement son objectif de faire comprendre l’abstrait ultime à qui n’en maîtrise pas les arcanes. Car pour comprendre, vous comprendrez! Il suffit (et à ce « suffit » suffit sa rigoureuse définition) de suivre le pas-à-pas proposé par D.F. Wallace, dans ce qui apparaît parfois comme d’inutiles ou ornementales circonvolutions, pour goûter à ce vertige qu’est comprendre.
est continue en 
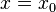si pour tout 
tel que
Même ce théorème de Weierstrass, qui contribue un peu plus à sortir l’analyse de l’ornière géométrique et éclaire d’une manière résolument définitive (sisi on vous assure) le problème épineux de la continuité, et donc remet au goût du jour la nécessité de définir ce qu’est un réel (sisi aussi), même ce théorème donc, qui vous parait sans doute résolument inatteignable, la lecture de cette histoire compacte vous le rendra aussi aisément saisissable qu’un poème de Maurice Carême. Et donc, vous sauvant de votre perplexité devant la célèbre dichotomie de Zénon, vous démontrera, si besoin en était, qu’il vous est non seulement loisible, mais aussi possible de, par exemple, traverser la rue. Rien de moins…
quelques abstraits que soient les systèmes infinis, après Cantor, ils ne sont certainement pas abstraits comme le sont les licornes, de manière non réelle/irréelles.
Articulant son projet d’histoire compacte autour des questions qui ont sous-tendu l’évolution des mathématiques vers les transfinis, il nous permet d’approcher le cheminement mathématique par le versant qui le légitime. Tout calcul suppose une réalité (une, ou une autre, quelle qu’elle soit et même simplement possible). Et le calcul, comme le langage, cette autre abstraction, suppose également que le réel, étant lui-même mis en jeu, puisse devenir, dans ces systèmes abstraits, non plus une aide ou un référent, mais une simple médiation, dont il convient parfois de douter. David Foster Wallace nous rappelle ici, et ce en toute décontraction (croyez-nous), que la chose mathématique a bien un statut ontologique.
Faisons tous une pause pendant un instant afin d’imaginer à quoi peut bien ressembler l’intérieur de la tête du professeur G.F.L.P. Cantor pendant qu’il démontre des trucs de ce genre.
David Foster Wallace, Tout et plus encore. Une histoire compacte de l’infini, 2011, Ollendorff & Desseins, trad. Thomas Chaumont.
envoi en cours...